Introducción
Los Modelos de Lenguaje Pequeños (SLMs) han sido un tema de gran interés, especialmente en la resolución de problemas matemáticos complejos. Un estudio reciente realizado por investigadores de Microsoft («Orca-Math: Unlocking the potential of SLMs in Grade School Math«) ha llevado esta discusión a un nuevo nivel con un modelo que desafía las limitaciones previas de los SLMs en el benchmark GSM8K.
Orca-Math: Un Nuevo Avance en SLMs
Orca-Math es un Modelo de Lenguaje Pequeño (SLMs), diseñado específicamente para abordar el desafío de la resolución de problemas matemáticos de palabras a nivel de escuela primaria. Este modelo, con una arquitectura de 7 mil millones de parámetros basada en Mistral-7B, destaca por su capacidad excepcional para alcanzar una precisión notablemente alta (86,81%) en el benchmark GSM8K, un conjunto de datos de referencia para evaluar el razonamiento matemático en IA.
La clave del éxito de Orca-Math radica en su enfoque único para el entrenamiento y la generación de datos. En lugar de depender de múltiples llamadas a modelos más grandes o herramientas externas para realizar cálculos o corregir errores (como programas que ejecutan código Python para realizar cálculos matemáticos precisos, o verificadores que revisan y corrigen las respuestas generadas por el modelo), Orca-Math utiliza un conjunto de datos sintéticos de alta calidad y técnicas avanzadas de entrenamiento iterativo para mejorar continuamente su precisión en la resolución de problemas matemáticos complejos.
a) Creación del dataset de entrenamiento mediante «Agent-Instruct»
El estudio utilizó un conjunto de datos sintético de alta calidad de 200K problemas matemáticos, generado mediante un sistema multiagente denominado «Agent-Instruct». Este sistema no solo parafrasea problemas existentes, sino que también incrementa su diversidad y dificultad.
Agentes Clave en el Entrenamiento mediante «Agent-Instruct»
- Agent – Ask Me Anything: Este agente se encargó de expandir el conjunto inicial de problemas, creando múltiples problemas a partir de cada uno en el conjunto de semillas.
- Agentes – Suggester & Editor: Estos agentes colaboraron para desarrollar problemas más desafiantes, incrementando la complejidad de los problemas existentes a través de un proceso iterativo.
Este enfoque multifacético aseguró que el dataset final no solo fuera grande, sino también variado y desafiante, cubriendo un amplio espectro de dificultades matemáticas.
b) Entrenamiento y Aprendizaje Iterativo de Orca-Math
El proceso de entrenamiento de Orca-Math fue igualmente innovador. Comenzando con un entrenamiento supervisado (SFT) con el dataset creado por el «Agent-Instruct», el modelo luego pasó por ciclos de generación de soluciones y retroalimentación, lo que permitió una mejora constante en su precisión.
Etapas de Entrenamiento
- Entrenamiento Supervisado (SFT): Orca-Math fue primero afinado con el dataset Orca-Math, logrando una precisión inicial del 81.50% en GSM8K en la métrica pass@1.
- Aprendizaje Iterativo: El modelo pasó por ciclos adicionales de generación de soluciones y retroalimentación. Se generaron múltiples respuestas para cada problema, y estas respuestas fueron evaluadas y comparadas con las soluciones del ‘maestro’ (GPT-4 Turbo). Este ciclo de retroalimentación permitió al modelo aprender tanto de respuestas positivas (correctas) como negativas (incorrectas), mejorando aún más su precisión.
Evaluación de la Precisión de Orca-Math en GSM8K
Una faceta crucial del estudio Orca-Math fue cómo se midió su rendimiento en el benchmark GSM8K, un conjunto de datos estándar para evaluar la capacidad de razonamiento matemático de los modelos de IA. Para esta evaluación, se utilizó una métrica específica conocida como la coincidencia exacta basada en GPT-4.
Métrica de Coincidencia Exacta Basada en GPT-4
La precisión de Orca-Math se midió utilizando un enfoque de coincidencia exacta, donde las respuestas generadas por el modelo se comparaban directamente con las respuestas correctas. Esta técnica se basa en la capacidad de GPT-4 para extraer la respuesta corta final de una solución más larga y luego compararla con la respuesta ‘de oro’ proporcionada en el GSM8K.
Este método de evaluación es particularmente riguroso, ya que requiere que la respuesta generada por el modelo coincida exactamente con la respuesta correcta. No hay margen para variaciones o interpretaciones, lo que significa que la precisión reportada refleja una verdadera coincidencia entre la solución del modelo y la solución estándar.
Importancia de Esta Metodología de Evaluación
Esta metodología de evaluación rigurosa es esencial para entender el logro significativo de Orca-Math. Al alcanzar una precisión del 86.81% en GSM8K utilizando esta métrica de coincidencia exacta, Orca-Math no solo demostró su capacidad para resolver problemas matemáticos de forma precisa, sino que también validó su eficacia en generar respuestas que son exactamente correctas, un desafío notable en el campo de la inteligencia artificial.
Resultados y Comparativas
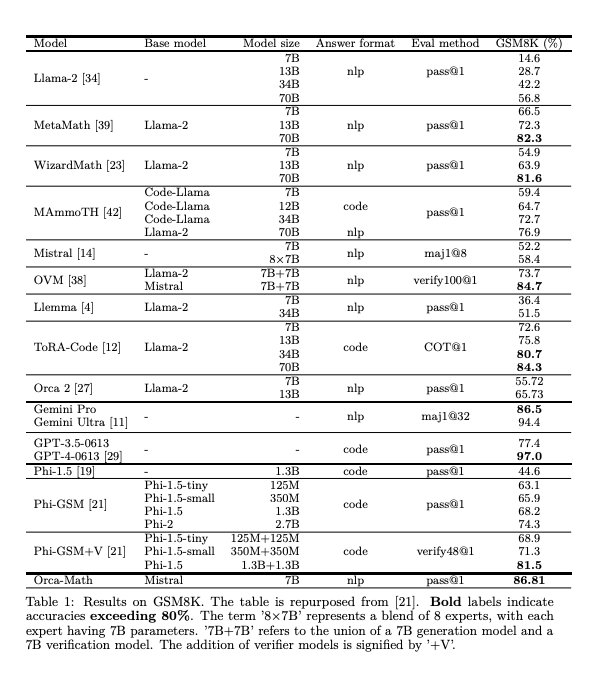
Orca-Math logró una precisión final del 86.81% en GSM8K, superando no solo su rendimiento inicial sino también el de modelos mucho más grandes. Es importante destacar que este nivel de precisión se logró sin necesidad de múltiples llamadas al modelo o el uso de herramientas externas, un logro notable dado el tamaño relativamente pequeño del modelo.
En comparación con modelos más grandes como LLAMA-2-70B, WizardMath-70B y GPT-3.5, Orca-Math no solo superó sus resultados en GSM8K, sino que también demostró ser más eficiente en términos de uso de datos, logrando estos resultados con solo 200K ejemplos, mucho menos que otros datasets. Este resultado es significativo, ya que demuestra que los modelos más pequeños y eficientes en datos pueden alcanzar o incluso superar la capacidad de modelos mucho más grandes y costosos.
Impacto y Futuro de los SLMs en la Resolución de Problemas Matemáticos
La metodología detrás de Orca-Math representa un avance significativo en el campo de los SLMs. A través de un enfoque innovador en la generación de datos y un proceso de aprendizaje iterativo y reflexivo, Orca-Math no solo ha establecido un nuevo estándar en la precisión de la resolución de problemas matemáticos por parte de los SLMs, sino que también ha abierto nuevas vías para explorar en la educación y otras aplicaciones prácticas de la inteligencia artificial.
Aplicaciones en el Contexto Educativo
En el ámbito educativo, los hallazgos de Orca-Math abren la puerta a nuevas posibilidades. Los SLMs como Orca-Math podrían usarse para desarrollar herramientas educativas personalizadas y accesibles, ofreciendo a los estudiantes asistencia en tiempo real para resolver problemas matemáticos y proporcionando explicaciones detalladas.
Aplicaciones Prácticas en Diversos Campos
Más allá del aula, los principios detrás de Orca-Math tienen el potencial de ser aplicados en una variedad de contextos donde la resolución de problemas y el análisis lógico son cruciales. Esto incluye campos como la programación, la ingeniería y la investigación científica, donde los modelos de IA pueden asistir en la solución de problemas complejos, la optimización de procesos y la toma de decisiones basadas en datos.
